Global Models of Surface Wave Group Velocity

We have inverted for models of surface wave group velocity at periods between 35 s and 175 s. The method and results are described in Larson & Ekström (2001). We inverted separately for Love and Rayleigh waves at each period for a model parameterized with spherical harmonics up to degree 40.

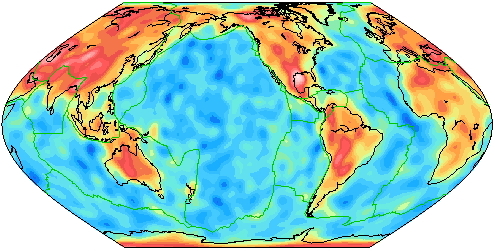35-second Love wave group velocity map of perturbations with respect to PREM.

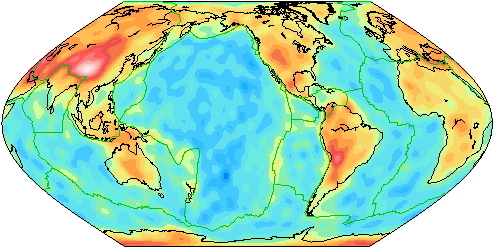35-second Rayleigh wave group velocity map of perturbations with respect to PREM.

• Larson, E.W.F., & Ekström, G., 2001.
  Global models of surface wave group velocity.
  Pure Appl. Geophys. 158, 1377-1400.

Phase Velocity Maps

We have automatically measured phase dispersion and arrival angles on seismograms from a database of over 100,000 digital records. The measurements are in the range 32s to 150s. This data set is inverted for global laterally heterogeneous phase velocity structure. We have developed theory for interpreting the measurements in terms of anisotropic phase velocity.

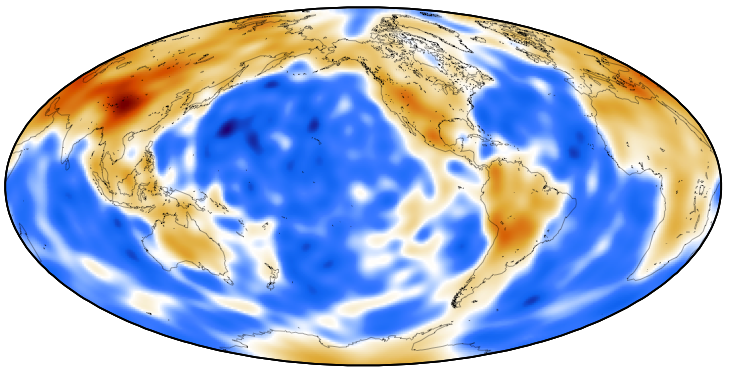35-second Love wave phase velocity map of perturbations with respect to PREM.

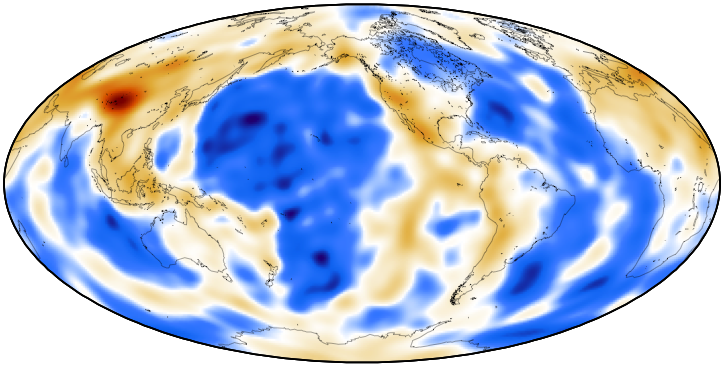35-second Rayleigh wave phase velocity map of perturbations with respect to PREM.

• Ekström, G., Tromp, J., & Larson, E.W.F., 1997.
  Measurements and global models of surface wave propagation.
  J. Geophys. Res. 102, 8137-8157.

Normal-Mode Observations

Measurements of the central frequency, Q, and splitting of various spheroidal and toroidal modes have been made, and are available here.

• He, X., & Tromp, J., 1996.
  Normal-mode constraints on the structure of the mantle and core.
  J. Geophys. Res. 101, 20,053-20,082.
• Tromp, J., & Zanzerkia, E., 1995.
  Toroidal splitting observations from the great 1994 Bolivia and Kuril Islands earthquakes.
  Geophys. Res. Lett. 22, 2297-2300.

Back to other research projects.