Properties of the Earth's Core

The Earth's inner core has this remarkable property: Compressional waves travel faster along its spin axis than in the equatorial plane. Such a directional dependence of wave propagation, together with the anomalous splitting of core-sensitive normal modes, was explained by an anisotropic inner core model first proposed by Harvard Seismology Group in 1986. Since then, we have further investigated its anisotropy extensively using both travel-time anomalies and the normal modes splitting.

Interdisciplinary Investigation of the Inner Core

Advances in ab initio or first-principles calculations of iron alloy at core temperatures and pressures are allowing direct comparison of alloy properties with seismological observations. We collaborate with mineral physicists to consider the seismic properties, iron alloy properties, and evolution of the inner core.

Bridging gap between mineral physics and seismology Ab initio calculations of the iron alloy determines density and elastic tensor of the alloy whereas seismological observations provide values of density and average wave speeds based upon travel-time measurements and free-oscillations. We formulate how to relate the crystalline properties to seismological observations. Composition of the inner core By matching average and anisotropic properties of iron alloys predicted by ab initio calculations with seismological observations, composition of the inner core is investigated. Evolution of the inner core Radial changes in observed anisotropy is related to changes in alignment of crystals which is then interpreted in terms of the evolution of the inner core.

Innermost Inner Core

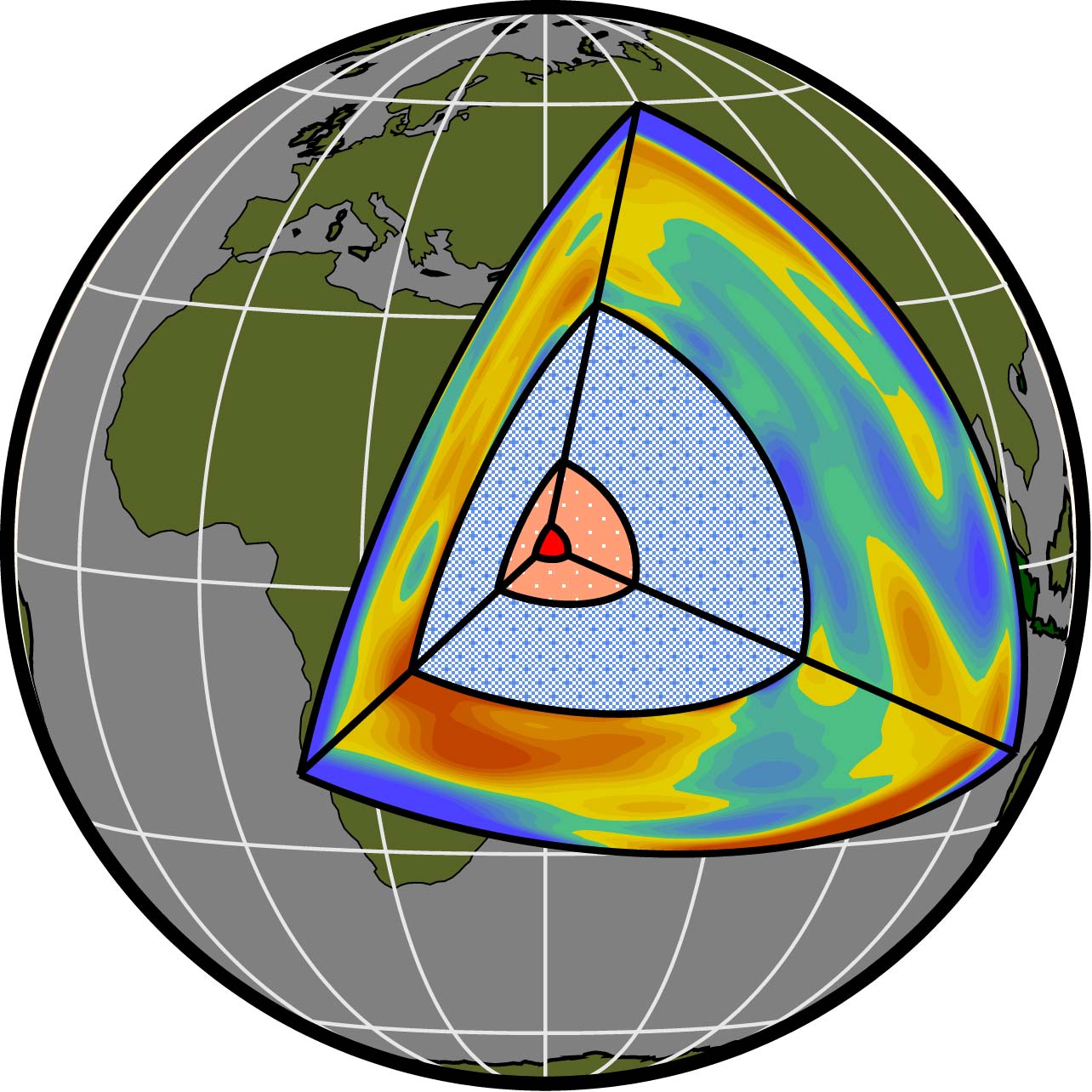Travel-time anomalies of waves traversing the inner core indicate that the directional dependence of wave propagation within the inner core is generally fast for waves travelling in the north-south direction, and low for waves travelling in the equatorial plane. This is consistent with normal-mode splitting data. However, the anomalies associated with antipodal data (173-180 degrees), sampling the deepest part of the inner core, show a different behaviour, with the fastest direction that is about 45 degrees from the rotation axis. The anisotropy is also much stronger than indicated by travel-time anomalies at smaller distances. This change in anisotropy is interpreted as a different layer within the inner core (the innermost inner core) that is about 300 km in radius at the centre of the Earth. (left) Cut-in view of the Earth's interior indicating heterogeneous mantle (upper layer with red and blue variations showing slow and fast seismic wave speed anomalies), outer core (blue region), bulk inner core where the fast axis coincides with the rotation axis (pink region), and innermost inner core where the fast axis does not coincide with the rotation axis (red region).

Structure of the Outer Core

Taylor cylinder structure Using splitting data of core-sensitive modes, the strength of heterogeneity within the outer core associated with Taylor cylinder structure is tested. Outer core structure and mantle anisotropy Seismic tomography can produce laterally-varying structure within the outer core to fit core-sensitive body-wave data, but this can be an artifact due to imperfect modelling of mantle structure.

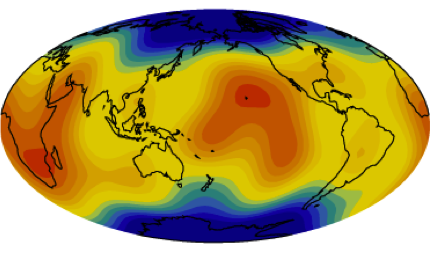Splitting function of mode 6S3 that is sensitive to structure in the inner core to the surface.

Anisotropy Model of the Inner Core

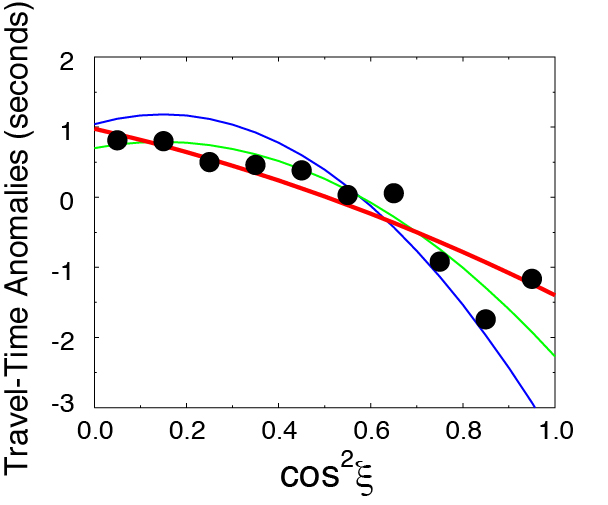Comparison of PKIKP travel-time anomalies (at a distance range of 150 to 153 degrees) binned by the ray angle ξ (black circles) with three inner-core anisotropy models.

Joint Modelling of Travel Times and Mode Splitting Anisotropy models of the inner core based upon body-wave and free-oscillation data show significant differences, especially in the strength of anisotropy. In order to obtain a model that can reconcile both types of data, mode splitting data are combined with absolute and differential travel-time measurements in the inversion. The resulting model can explain much of the data, and also identifies anomalous paths. Anomalous Splitting of Normal Modes Splitting of inner-core sensitive normal modes show strong zonal dependence unlike mantle modes that tend to have strong degree 2 order 2 component. This signal is explained by a cylindrical anisotropy model of the inner core. PKIKP Travel-Time Anomalies Travel-time anomalies associated with the inner core show dependence on the angle each ray path makes with the Earth's rotation axis. This observation is explained by a cylindrical anisotropy model of the inner core.

Three Dimensionality of Inner-Core Anisotropy

In order to investigate lateral variations in anisotropy, a cylindrical anisotropy stacking procedure is developed to analyze the travel-time data. In order to use the stacked data, a compressional velocity perturbation formula is derived for a hexagonally close-packed medium with random spatial orientation to relate three-dimensional anisotropic effects to travel-time residuals. The data are inverted for an anisotropy pattern which can be used to explore possible mechanisms of inner-core anisotropy.

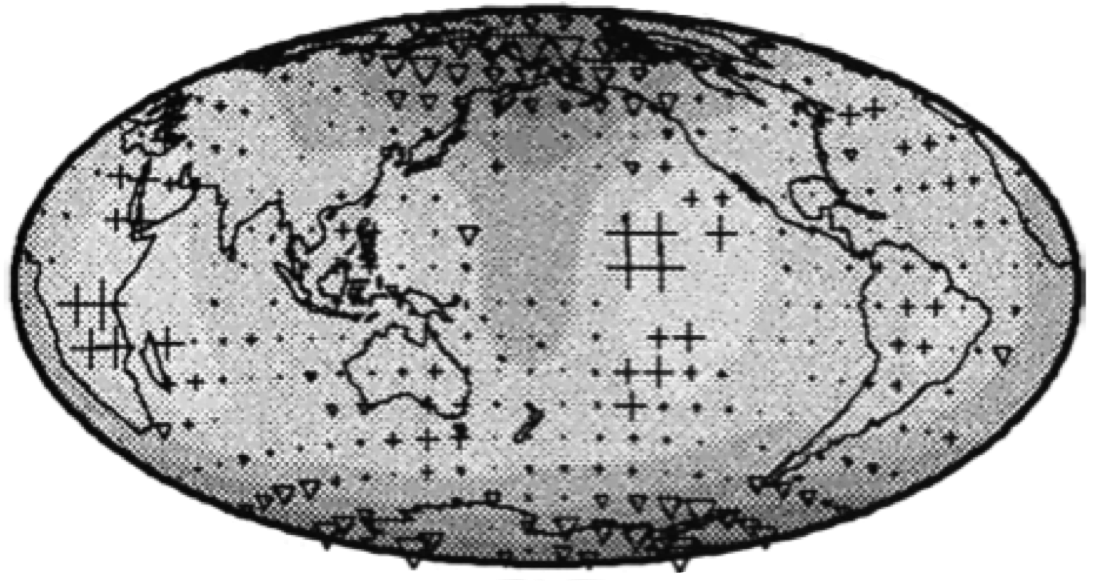Cylindrical anisotropy stacks of PKIKP residuals calculated for a distance range between 156 and 160 degrees. The plus symbols indicate positive anomalies, and inverted triangles indicate negative anomalies. The size of the symbol is showing the size of the residual.

Axis of Symmetry

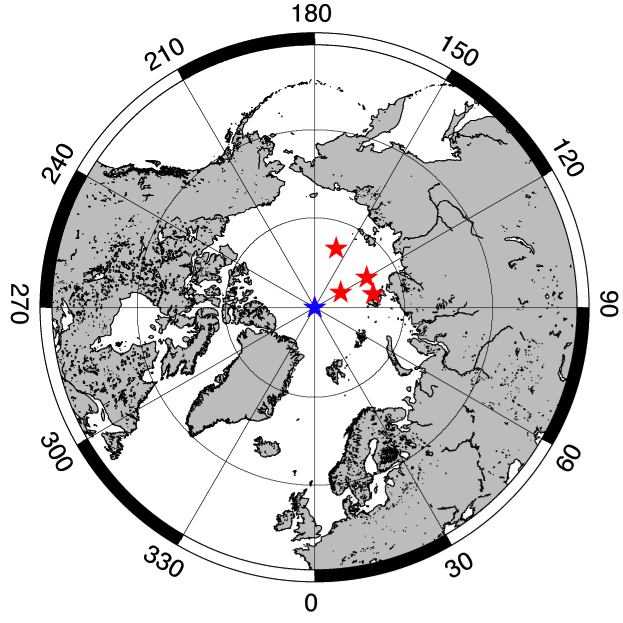The travel-time anomalies associated with the inner core can generally be explained by the axis of symmetry being aligned with the rotation axis. The fit to the data can be improved by tilting the axis of symmetry away from the rotation axis, to a location of 79.5 N latitude and 160 S longitude. However, the axis location is not very well constrained, and similar level of data fit can be achieved by axes at slightly different locations. (left) Comparison of the inner-core anisotropy symmetry axes projected to the Earth's surface in the northern hemisphere. The blue star indicates the rotation axis, and red stars show potential axis locations.

Temporal Variation of Inner-core Anisotropy

Temporal variations of the ISC travel-time residuals are investigated which revealed a differential rotation of the inner core relative to the mantle at a rate of about 3 degree faster per year. (left)PKIKP travel-time anomalies that have been cylindrically averaged. The yellow triangles show negative anomalies and blue inverted triangles show positive anomalies. The size of the triangles indicates the size of the travel-time residuals. The top panel shows the distribution of the residuals obtained from data between 1974 and 1978, and the bottom figure shows the same data but from years between 1988 and 1992.

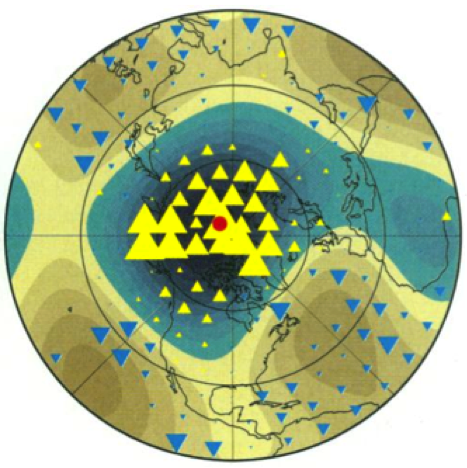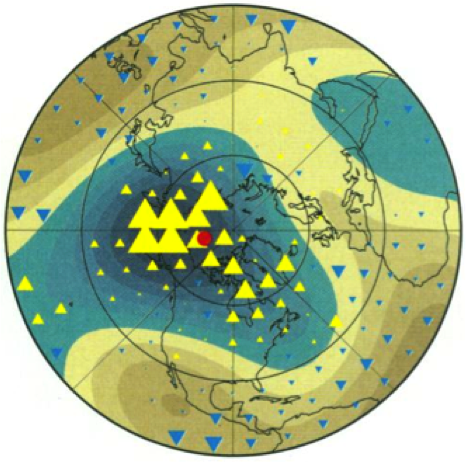Publications

Ishii, M., 2007.
Seismological constraints on the structure of the Earth's core.
in Superplume: Beyond Plate Tectonics, edited by D. Yuen, S. Karato, S. Maruyama, & B.F. Windley, pp. 31-68, Kluwer Academic Press, New York.

Ishii, M., & Dziewoński, A.M., 2005.
Constraints on the outer core tangent cylinder using normal-mode splitting measurements.
Geophys. J. Int. 162, 787-792, doi:10.1111/j.1365-246X.2005.02587.x.

Ishii, M., & Dziewoński, A.M., 2003.
Distinct seismic anisotropy at the centre of the Earth.
Phys. Earth Planet. Inter. 140, 203-217.

Ishii, M., & Dziewoński, A.M., 2002.
The innermost inner core of the Earth: Evidence for a change in anisotropic behaviour at the radius of about 300 km.
Proc. Natl. Acad. Sci. USA 22, 14026-14030.

Ishii, M., Tromp, J., Dziewoński, A.M., & Ekström, G., 2002.
Joint inversion of normal mode and body wave data for inner core anisotropy: 1. Laterally homogeneous anisotropy.
J. Geophys. Res. 107, 10.1029/2001JB000712.

Ishii, M., Dziewoński, A.M., Tromp, J., & Ekström, G., 2002.
Joint inversion of normal mode and body wave data for inner core anisotropy: 2. Possible complexities.
J. Geophys. Res. 107, 10.1029/2001JB000713.

Boschi, L., & Dziewoński, A.M., 1999.
Whole Earth tomography from delay times of P, PcP, and PKP phases: Lateral heterogeneities in the outer core or radial anisotropy in the mantle?
J. Geophys. Res. 105, 13675-13696.

Su, W.-J., Dziewoński, A.M., & Jeanloz, R., 1996.
Planet within a planet: Rotation of the inner core of Earth.
Science 274, 1883-1887.

Su, W.-J., & Dziewoński, A.M., 1995.
Inner core anisotropy in three dimensions.
J. Geophys. Res. 100, 9831-9852.

Tromp, J., 1995.
Normal-mode splitting observations from the Great 1994 Bolivia and Kuril Islands earthquakes: Constraints on the structure of the mantle and inner core.
GSA Today 5, 137-151.

Tromp, J., 1995.
Normal-mode splitting due to inner-core anisotropy.
Geophys. J. Int. 121, 963-968.

Tromp, J., 1993.
Support for anisotropy of the Earth's inner core from free oscillations.
Nature 366, 678-681.

Morelli, A., & Dziewoński, A.M., 1987.
Topography of the core-mantle boundary and lateral homogeneity of the liquid core.
Nature 325, 678-683.

Morelli, A., Dziewoński, A.M., & Woodhouse, J.H., 1986.
Anisotropy of the inner core inferred from PKIKP travel times.
Geophys. Res. Lett. 13, 1545-1548.

Woodhouse, J.H., Giardini, D., & Li, X.-D., 1986.
Evidence for inner core anisotropy from free oscillations.
Geophys. Res. Lett.13, 1549-1552.

Back to other research projects.